Bibliography

1

S. Brackin, C. Meadows, and J. Millen, ``CAPSL Interface for the NRL Protocol Analyzer'' , IEEE Symposium on Application-Specific Systems and Software Engineering Technology (ASSET '99, Dallas, March 1999)

2

B. Boyer, M. Kaufmann and J.S. Moore
The Boyer-Moore theorem prover and its interactive enhancement.
Computers and Mathematics with Applications, Vol. 29, No. 2, pp. 27-62, 1995.

3

A. Camilleri, M. Gordon, and T. Melham.
Hardware verification using higher order logic.
In D. Borrione, editor, HDL Descriptions to Guaranteed Correct Circuit Designs. Elsevier Scientific Publishers, 1987.

4

B. Char et. al, ``The Maple symbolic computation system'', SIGSAM Bulletin, vol. 17 1983), no. 3/4, pp. 31-42.

5

A. Church.
A formulation of the simple theory of types.
Journal of Symbolic Logic, 5, 1940.

6

Edward Cohen, Programming in the 90's: an introduction to the calculation of programs, Springer-Verlag, 1990.

7

R.L. Constable et. al.
Implementing Mathematics with the Nuprl Proof Development System.
Prentice Hall, 1986.

8

N. deBruijn, ``Lambda-calculus with nameless dummies, a tool for automatic formula manipulation, with application to the Church-Rosser theorem'', in Nederpelt, et. al., eds., Selected Papers on Automath, North Holland, 1994.

9

W.M. Farmer, J. D. Guttman and F. J. Thayer.
IMPS: An Interactive Mathematical Proof System (system abstract)
10th International Conference on Automated Deduction, pp. 653-654, 1990.

10

Gordon, M. J. C., Milner, R., and Wadsworth, C. P. Edinburgh LCF: A Mechanised Logic of Computation, Volume 78 of Lecture Notes in Computer Science. Springer-Verlag, 1979.

11

M. Gordon.
A proof generating system for higher-order logic.
Technical Report 103, University of Cambridge Computer Laboratory, January 1987.

12

David Gries and Fred B. Schneider, A Logical Approach to Discrete Math, Springer-Verlag, 1993.

13

M. Randall Holmes, ``Systems of combinatory logic related to Quine's `New Foundations' '', Annals of Pure and Applied Logic, 53 (1991), pp. 103-33.

14

M. Randall Holmes, ``A functional formulation of first-order logic `with infinity' without bound variables'', preprint, available from the author.

15

M. Randall Holmes, ``Untyped 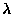$\lambda$-calculus with relative typing, in Typed Lambda-Calculi and Applications (proceedings of TLCA '95), Springer, 1995, pp. 235-48.

16

M. Randall Holmes, ``The Mark2 Theorem Prover'', final progress report of Army Research Office grant DAAH04-94-0247.

17

M. Randall Holmes, Elementary Set Theory with a Universal Set, Academia-Bruylant, Louvain-la-Neuve, 1998.

18

Jech, Thomas, ``OTTER experiments in a system of combinatory logic'', Journal of Automated Reasoning, 14, pp. 413-426.

19

Ronald Bjorn Jensen, ``On the consistency of a slight (?) modification of Quine's `New Foundations' '', Synthese, 19 (1969), pp. 250-63.

20

D. Kapur and H. Zhang,.
An overview of RRL (Rewrite Rule Laboratory)
Proc. of Third International Conf. of Rewriting Techniques and Applications, Chapel Hill, North Carolina, April 1989.

21

Knuth, D. and Bendix, P., ``Simple word problems in universal algebras'', in Computational Problems in Abstract Algebra (ed. Leech), Pergamon Press, 1970, pp. 263-97.

22

W. McCune.
Otter 3.0 Reference Manual and Guide
Technical Report ANl-94/6, Argonne National Laboratory (1994).

23

Milner, et. al, The Definition of Standard ML (Revised), MIT Press, 1997.

24

Nederpelt, et. al., eds., Selected Papers on Automath, North Holland, 1994.

25

W. V. O. Quine, ``New Foundations for Mathematical Logic'', American Mathematical Monthly, 44 (1937), pp. 70-80.

26

Syverson, Paul F. and Paul C. van Oorschot. ``On Unifying Some Cryptographic Protocol Logics'', Proceedings of the 1994 IEEE Computer Society Symposium on Research in Security and Privacy Oakland CA May 1994, IEEE CS Press (Los Alamitos, 1994)

27

Stephen Wolfram, Mathematica: A System for Doing Mathematics by Computer, Addison-Wesley, 1988